例子1：ZOJ-1004-Anagrams by Stack

问题找出一个入栈、出栈序列，把字符串A变成B，有多个可能序列。这是回溯和栈的问题，我把这个问题在一棵Push-Pop树上的遍历问题:

data Tree a = Empty
            | Node a (Tree a) (Tree a)

data Action = Push | Pop deriving (Eq, Ord)

pushPopTree :: Tree Action
pushPopTree = let popTree = Node Pop popTree pushTree
                  pushTree = Node Push popTree pushTree
              in pushTree

上面得到pushPopTree是这样的：

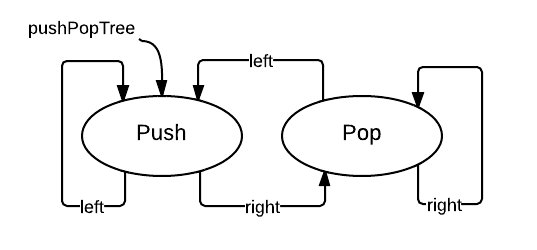
看起来不像树啊，部分展开之后就是这样的：

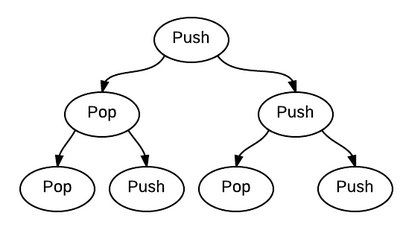
实际上，我们不需要展开，只要跟着指针遍历就可以：

dfsPushPopStr :: String -> String -> [[Action]]
dfsPushPopStr strA strB
     | length strA /= length strB = error "string length must be equal"
     | otherwise = dfsPushPopStr' strA [] pushPopTree (0, 0) []
  where
    maxPush = length strA

    dfsPushPopStr' strA stack (Node x l r) (pushCount, popCount) currPath
        | popCount > pushCount || popCount + pushCount > 2 * maxPush = []
        | x == Pop = if popCount + 1 == pushCount
                        && pushCount == maxPush && newStrA == strB
                         then [currPath ++ [x]]
                         else go r ++ go l
        | x == Push = if popCount == maxPush
                         then []
                         else go r ++ go l
      where
        go tree  = dfsPushPopStr' newStrA newStack
		             tree nextCount nextPath
        nextPath = currPath ++ [x]
        (newStrA, newStack) =
            case x of
              Pop  -> (strA ++ [head stack], tail stack)
              Push -> (tail strA, head strA : stack)
        nextCount =
            case x of
              Pop  -> (pushCount, popCount + 1)
              Push -> (pushCount + 1, popCount)

dfsPushPopStr'是本体，参数略多，就是在遍历的时候记录路径是Push和Pop的个数，根据节点进行相应的栈操作，然后继续遍历。

例子2：换硬币问题

就是换零钱，假设有足够的5角、1元、5元、10元、20元，问N元有多少种换的方法。这个问题不难，简单地递归就能求出种数。现在我要生成全部的替换方式。我本来想在原来求种数的基础上输出替换方式，失败了。然后我一棵树表示全部的替换方式，然后在树上遍历。

data Tree = Tree Int [Tree]

makeTrees :: [Int] -> [Tree]
makeTrees [] = []
makeTrees (x:xs) =
    let ts = makeTrees xs
        tx = let t = Tree x (t:ts) in t
    in tx : ts

makeTrees [5,10, 50, 100, 200]就能生成问题所需的树，这树画起来要比上一例复杂，但是遍历简单：

exchange' total !curr !path (Tree x trees)
    | total == curr + x = tell [x:path]
    | total < curr + x = return ()
    | otherwise = mapM_ (exchange' total (curr + x) (x:path)) trees

exchange total coins = execWriter $
    mapM_ (exchange' total 0 []) (makeTrees coins)

模式

上面的两个例子都是先生成一棵树，然后遍历，相当于把算法里隐含的遍历模式显式表示出来。牛人大概不会这样写，但是我发现当我把树写出来后，我对算法遍历的模式就有更直观的理解。

显式遍历模式

例子1：ZOJ-1004-Anagrams by Stack

例子2：换硬币问题

模式